Low-Dimensional Case

MCHMC conserves the energy, which in 1D is equal to:

\[ E = \log \Pi(t) - \log p(x(t)) \]

so that

\[ \Pi(t) \propto 1/p(x(t)). \]

We will take the initial condition \(x(0) = -\infty\) with the proportionality constant equals 1 in the above relation and periodic boundary conditions at infinity. The Hamilton's equation for the velocity gives \(\dot{x} = 1/p(x(t)\), so for \(0 \leq t \leq 1\):

\[ t = \int_{-\infty}^{x(t)} p(x) dx = P(X < x(t)) \]

and the general solution is

\[ x(t) = \mathrm{CDF}^{-1}(t \, \mathrm{mod} \, 1). \]

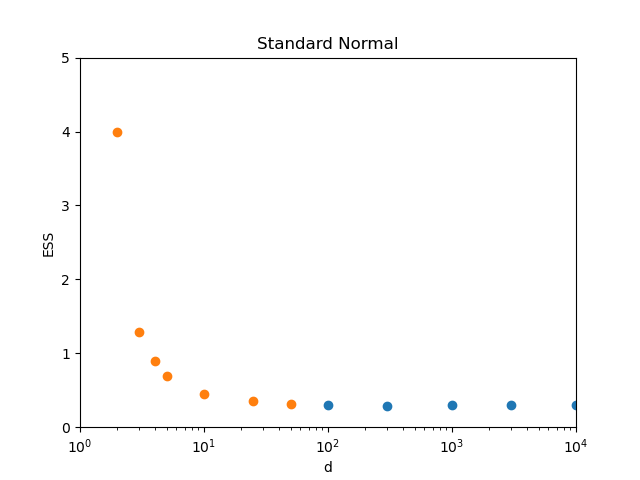
With some \(\epsilon\) stepsize in time, this is the improved inverse transform sampling¹, where a random number generator was replaced by a low-discrepancy sequence² generator, namely the additive recurrence. As such, it is very efficient and has \(ESS > 1\). This property persists in dimensions \(d = 2\) and \(d = 3\) as is shown in Figure 1 with the standard Gaussian target in various dimensions.